Introducción
Desde hace varios años la literatura científica reconoce la existencia de una relación entre el estímulo de entrenamiento y la adaptación del atleta (Banister EW, Calvert TW, Savage MV. A systems model of training for athletic performance), esta relación se puede modelizar mediante lo que se conoce como Modelo de Impulso-Respuesta.La carga de entrenamiento se puede expresar como:
Carga de entrenamiento = Intensidad * DuraciónExisten diferentes maneras de cuantificar el estímulo de entrenamiento, uno de los mas utilizados fue propuesto por el propio Dr. Eric Banister en la década del '70 y se basa en relacionar la frecuencia cardíaca con la concentración del lactato en sangre mediante un estudio poblacional, esto tiene mucho sentido considerando la importancia que de la potencia al umbral de lactato como determinante primario del rendimiento en deportes de resistencia y la relación entre los niveles de lactato en sangre y los procesos metabólicos que tienen lugar.
La principal ventaja de este esquema es que toma en consideración la relación no lineal (exponencial) que existe entre la intensidad de entrenamiento y el stress que provoca.
La desventaja es que depende de la medición de la frecuencia cardíaca que es una variable dependiente no solo de la intensidad de entrenamiento sino también de otros factores como la hidratación, descanso, enfermedad, ingestión de cafeína, etc.
Para superar esa limitación en 2003 el Dr. A.Coggan propuso un refinamiento del método de Banister consistente en utilizar la medición directa de la potencia mecánica (en ciclismo mediante medidores de potencia) y la relación entre la potencia y la concentración de lactato en sangre, esta nueva métrica, llamada Training Stress Score (TSS, marca registrada de PeaksWare LLC) se calcula como:
Tss = Duración * Potencia Promedio * Factor de intensidadEl factor de intensidad se obtiene a partir de la relación entre la concentración de lactato como % de la concentración de lactato al umbral en función de la potencia como % de la potencia al umbral, el trabajo de Coggan muestra una relación de 4ta potencia entre ambos.
La correlación existente entre la potencia que se puede sostener durante 1h y el MLSS permite utilizar una prueba de campo y no depender de test de laboratorio.
La literatura sobre el entrenamiento de carrera muestra el mismo tipo de correlación entre el MLSS y el ritmo promedio en un prueba de ~1h de duración (ritmo de medio marathon para corredores de elite mundial, de 15km/10mi para amateurs de nivel medio y de 10km para amateurs de menor nivel).
El trabajo del Dr. Skiba extiende esta idea a la carrera utilizando los registros de velocidad y altimetría recopilados mediantes sistemas basados en GPS y/o acelerómetros y datos antropométricos para calcular la potencia en base a las publicaciones existentes en la materia.
Cálculo de la potencia de carrera
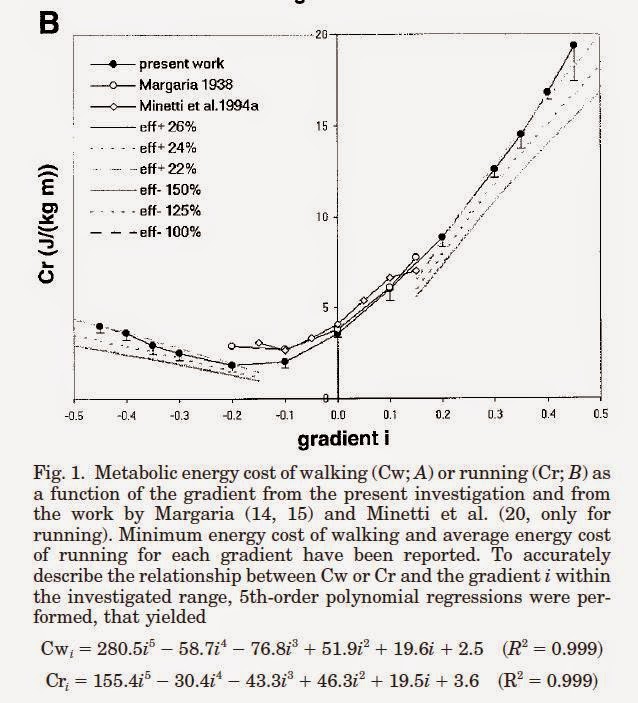
La potencia que se pone en juego para correr a una velocidad V se puede estimar como:Potencia = (eff * Cslope + Caero + Ckin) * VCslope es el componente principal en la carrera de fondo y depende de la inclinación del terreno de manera no-lineal pero es relativamente independiente de la velocidad de carrera:
donde: V es la velocidad calculada como distancia/tiempo, eff es la eficiencia, Cslope es el costo energético de propulsión en función de la pendiente, Caero el costo energético de vencer la resistencia aerodinámica y Ckin el costo energético asociado a los cambios de energía cinética asociados a la variación de la velocidad.
La componente aerodinámica juega un rol secundario debido a que depende del cuadrado de la velocidad y las velocidades no son suficientemente elevadas aunque la presencia de fuertes vientos puede alterar su magnitud y la componente asociada a los cambios de velocidad es la menos relevante. La eficiencia depende de la velocidad de manera relativamente compleja a los cambios en la recuperación de energía elástica y al cambio de la mezcla de carbohidratos y lípidos que se oxida. Debido a que los datos experimentales validan estas ecuaciones para distancias hasta los 800m se utiliza un promedio móvil de 120" para realizar los cálculos. Ver las referencia para mayores detalles.
Considerando la variabilidad
La variabilidad de los entrenamientos fraccionados o con cambios de ritmo tienen un rol muy importante en el impacto fisiológico del entrenamiento, para contemplar este efecto se aplica un promedio móvil a los datos de potencia teniendo en cuenta que muchos procesos fisiológicos (en particular el VO2) responden a estímulos con una vida media del orden de 30 segundos. En el siguiente gráfico se puede observar como la potencia normalizada, que utiliza promedios móviles de 30 segundos, aumenta cuando aumenta la variabilidad a pesar que la potencia promedio se mantiene constante: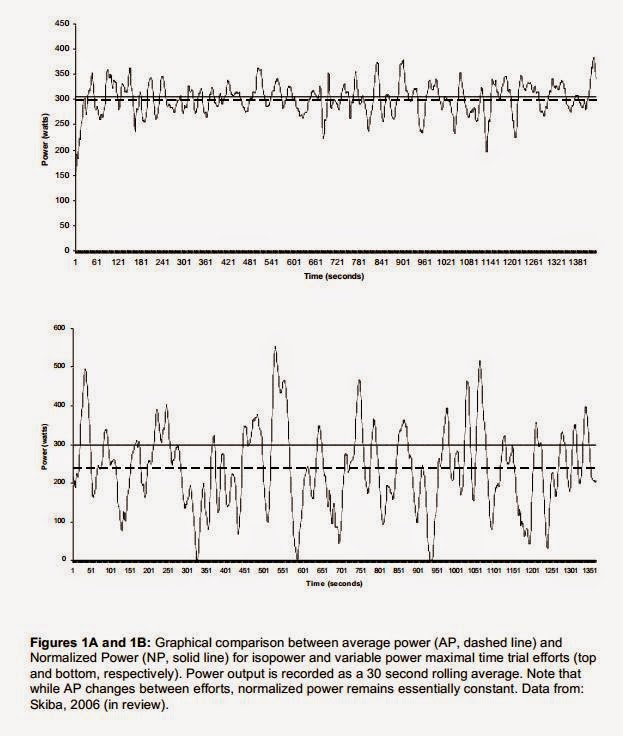
Considerando la Intensidad
Debido a la conocida relación entre la intensidad y el impacto fisiológico del ejercicio es conveniente "pesar" la intensidad tal como se describió en la introducción, para esto el Dr. Skiba propone utilizar la relación entre la concentración de lactato como % del umbral en función de la potencia o velocidad como % de la potencia o velocidad al umbral, el siguiente gráfico muestra datos experimentales y la correspondiente curva de regresión: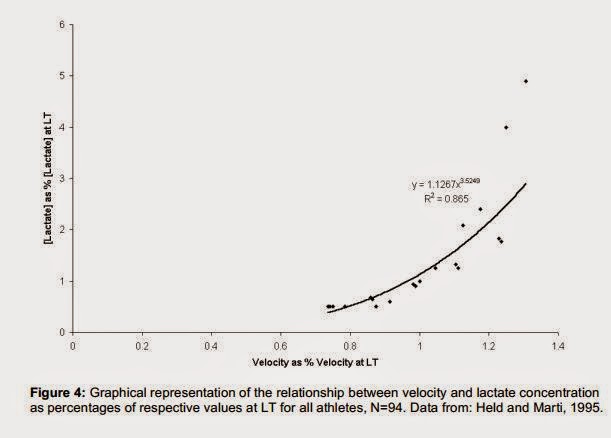
A los efectos de "pesar" la intensidad el exponente se redondea a 4.
Cálculo del GOVSS
El cálculo completo se realiza con los siguientes pasos:- Obtención de la velocidad al umbral del atleta correspondiente a 10k-21km según nivel
- Calcular la potencia correspondiente a esta velocidad
- Calcular la potencia en función de los promedios móviles de 120 segundos de velocidad y pendiente y aplicar un promedio móvil de 60 segundos.
- Elevar los valores del paso 3 a la potencia cuarta.
- Calcular el promedio de los valores del paso 4.
- Calcular la raíz cuarta del valor del paso 5. Este valor lo llamamos LNP.
- Dividir la potencia del paso 6 por la del paso 2, este valor es el factor de intensidad IWF.
- Multiplicar el LNP por la duración del entrenamiento para obtener el trabajo normalizado.
- Multiplicar el valor del paso anterior por el IWF
- Dividir los valores del paso anterior por el trabajo realizado durante 1h a velocidad de umbral (potencia dle paso 2 por 3600 segundos).
- Multiplicar los valores del paso anterior por 100 para obtener el GOVSS (Gravity Ordered Velocity Stress Score) .
Interpretación y Aplicaciones
Si bien los individuos difieren en su capacidad de adaptarse al entrenamiento en función de sus características individuales, antecedentes y carga previa se pueden establecer ciertos lineamientos generales sobre el impacto que produce un entrenamiento en función del GOVSS:Bajo - Recuperado para el día siguienteAdicionalmente estos valores se pueden utilizar como entrada para construir un Modelo Impulso Respuesta o un Modelo Gráfico Simplificado (PMC) a fin de tener una visión de conjunto de la evolución temporal de la carga de entrenamiento de carrera y su relación con el rendimiento.
75-125 Medio - Fatiga residual para el día siguiente
125-225 Alto - Alguna fatiga residual los próximos 2 días
>225 Muy Alto - Fatiga residual for más de 2 días
Ritmo Normalizado (xPace)
Una derivación potencialmente interesante de estos cálculos es la noción de "ritmo normalizado": la idea es que la LNP calculada en el proceso anterior está diseñada con el objetivo de representar la potencia equivalente desde el punto de vista de su impacto fisiológico si el entrenamiento completo hubiera sido desarrollado a intensidad constante y sin pausas.Por lo tanto podemos calcular el ritmo de carrera al que se hubiera desarrollado esa potencia en terreno llano y obtener lo que podríamos llamar "ritmo normalizado", es decir un ritmo contínuo que si se hubiera mantenido en el llano sin pausas por la duración del estímulo hubiera inducido un stress de entrenamiento equivalente, medido por GOVSS.
Implementaciones
Para realizar estos cálculos existen aplicaciones comerciales (RaceDay, TopoFusion) y de código abierto: GoldenCheetah a partir de la versión 3.2 disponible desde agosto de 2015 y que se puede descargar desde http://www.goldencheetah.org.Más Información
Mayores detalles y referencias bibliográficas: Calculation of Power Output and Quantification of Training Stress in Distance Runners: The Development of the GOVSS Algorithm del Dr. Philip Friere Skiba.Implementación de GOVSS/xPace en GoldenCheetah: https://github.com/GoldenCheetah/GoldenCheetah/blob/master/src/GOVSS.cpp
GOVSS (Gravity Ordered Velocity Stress Score) es una marca registrada de PhysFarm Training Systems LLC.








10 comentarios