 La versión 3 de Golden Cheetah presenta una interfaz de usuario mejorada y varias funciones nuevas, entre ellas la posibilidad de realizar una estimación automática del área de resistencia aerodinámica (CdA) y el coeficiente de resistencia a la rodadura (Crr) utilizando datos de pruebas de campo. La metodología propuesta por el Dr. Robert Chung e incluída en el módulo Aerolab de Golden Cheetah por Andy Froncioni, está aumentada en la versión 3 con un mecanismo de estimación de parámetros de mi autoría que se describe a continuación.
La versión 3 de Golden Cheetah presenta una interfaz de usuario mejorada y varias funciones nuevas, entre ellas la posibilidad de realizar una estimación automática del área de resistencia aerodinámica (CdA) y el coeficiente de resistencia a la rodadura (Crr) utilizando datos de pruebas de campo. La metodología propuesta por el Dr. Robert Chung e incluída en el módulo Aerolab de Golden Cheetah por Andy Froncioni, está aumentada en la versión 3 con un mecanismo de estimación de parámetros de mi autoría que se describe a continuación.
Para las pruebas necesitamos un medidor de potencia que registre valores instantáneos de velocidad y potencia correctamente calibrado y puesto a cero con el que dar una serie de vueltas a un circuito cerrado con las siguientes consideraciones:
- El circuito no necesita ser plano
- Velocidad y potencia no necesitan ser constantes
- Cuanto menos viento haya, mejor, idealmente en calma
- Se debe mantener la misma posición y no utilizar los frenos
La cantidad de vueltas dependerá de la longitud del circuito, más vueltas es mejor siempre que no lleve tanto tiempo como para que las condiciones varíen, con unos 10-15' de datos son suficientes y si el circuito es más corto podemos dar más vueltas.
Es conveniente que haya variación de velocidad, esto tenderá a ocurrir naturalmente si el circuito tiene variaciones de altura, si el circuito es relativamente llano hay que provocarlo, por ejemplo empezando a muy baja velocidad y acelerando progresivamente hasta la máxima velocidad que podamos mantener sin afectar la posición ni tener que usar los frenos.
Terminada la prueba descargamos los datos del medidor de potencia en Golden Cheetah (directamente o los importamos a partir de un archivo generado con el programa del medidor).
Una vez que tenemos los datos de la prueba, obtenidos de acuerdo a las recomendaciones de la nota anterior, cargados en Golden Cheetah V3 necesitamos acceder a los gráficos Aerolab y Editor que, sino están visibles, podemos agregar con el menú Ver->Agregar Gráfico->Análisis Chung Aerolab o mediante el botón (+) de la zona superior derecha:
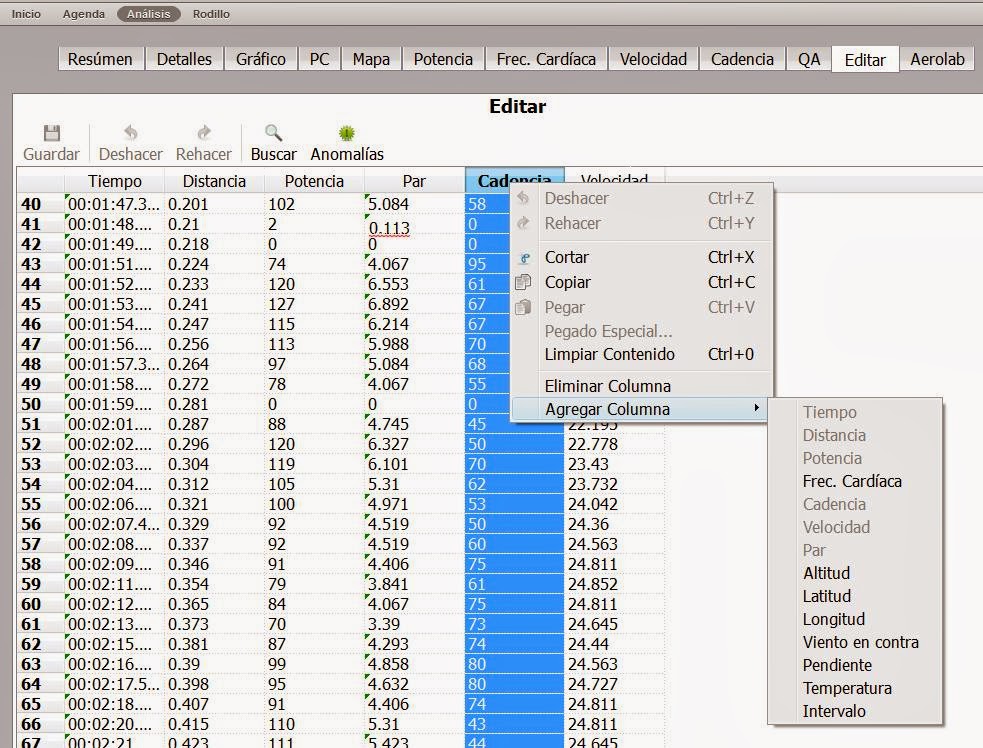
Si entre los datos no disponemos de la altitud, como es el caso en nuestro ejemplo, podemos utilizar el editor para agregar dicha columna:
Dado que el mecanismo de estimación automática utiliza el valor cero como indicador que la información de Altitud no está disponible debemos ingresar valores distintos de cero que delimiten los segmentos a utilizar en la estimación, el caso más sencillo (y recomendable) se presenta cuando se trata de vueltas alrededor de un circuito ya que en dicho caso solo necesitamos fijar la altitud en un punto del mismo una vez por vuelta (el valor no es relevante en la medida que sea el mismo en todos los casos y distinto de cero).
Una vez que guardemos las modificaciones estas quedarán reflejadas en Aerolab, como se puede ver en el siguiente ejemplo:
Otro dato importante es la densidad del Aire (Rho) que en la nueva versión también puede ser calculada por Golden Cheetah a partir de datos meteorológicos (temperatura, presión atmosférica y temperatura o punto de rocío) mediante Herramientas->Estimador de la Densidad del Aire:
Una vez actualizado este dato en Aerolab podemos utilizar el botón Estimar CdA y Crr para que el programa calcule los valores más adecuados para lograr la correspondencia entre la altimetría real y la virtual, para mejorar la visualización podemos corregir la Altimetría Inicial sin afectar los valores calculados, el resultado será similar al siguiente:
Para la estimación se utilizan los segmentos del recorrido comprendidos entre el primero y último punto con altimetría distinta de cero, de manera que es posible excluir la parte inicial y/o final simplemente dejando la altimetría de esos tramos en cero. Son necesarios dos segmentos independientes para poder realizar la estimación de manera que al menos tres puntos del recorrido deben tener altimetría distinta de cero.
Si el recorrido no es un circuito y contamos con datos de altitud en al menos 3 puntos del circuito (más es mejor en este caso) también podemos utilizarlos para realizar la estimación. La utilización de datos de altitud de GPS no es recomendable debido que no suelen tener la precisión necesaria (en este caso es preferible eliminar la columna de Altitud y agregar una nueva con datos manuales), por otro lado si los datos corresponden a un altímetro barométrico corregido en temperatura (o si la temperatura se mantuvo constante durante la prueba) probablemente puedan utilizarse directamente con resultados razonables.
Resumiendo podríamos afirmar que este método permite estimar los parámetros aerodinámicos y de resistencia a la rodadura mediante pruebas de campo sin necesidad de ajuste manual, como en el
método analítico, combinado con la flexibilidad y el carácter más intuitivo del
método gráfico que permite visualizar que tan bueno es el ajuste del modelo a las condiciones experimentales.
Para una presentación más detallada del método gráfico ver:
Determinación del Área de Resistencia Aerodinámica (CdA) mediante Pruebas de Campo: Método Gráfico
Anexo - Desarrollo Matemático
En su libro de divulgación A Brief History of Time - From the Big Bang to Black Holes, Stephen Hawking cuenta que su editor le dijo que por cada ecuación el universo de lectores se reduciría a la mitad, de manera que eliminó todas menos una (E=mc^2). Dado que carezco del enorme talento de Hawking voy a necesitar más de una ecuación para explicar un tema incomparablemente más simple y, a riesgo de perder lectores, las voy a incluir en este anexo, que si bien no es esencial para poder utilizar el método comentado en la parte principal, puede ser útil para comprender sus fundamentos.
La idea es contar con un número (mayor o igual a dos) de segmentos con la siguiente información:
- altimetría y velocidad inicial
- altimetría y velocidad final
- potencia, velocidad y viento frontal en los puntos intermedios.
Estos segmentos quedan definidos por aquellos puntos donde la altimetría es distinta de cero, un valor cero en la altimetría es considerado como ausencia de información, en el caso límite donde todos los puntos tienen altitud distinta de cero cada intervalo de grabación es considerado como un (mini) segmento.
Si el campo correspondiente al viento frontal (HeadWind) no está disponible se asumen condiciones de calma (HeadWind = v, donde v es la velocidad).
Con esta información y asumiendo que no se utilizan los frenos, no hay cambios en la posición, densidad del aire, masa total, etc. podemos calcular un balance de energía para cada segmento de manera independiente, donde la pérdida de energía compuesta por la pérdida debido al rozamiento aerodinámico (Aero-Loss) y la resistencia a la rodadura (Rolling-Loss), se equilibra con la ganancia debido a la potencia (Power) aplicada por el ciclista (menos las pérdidas de transmisión - Eta) multiplicada por la duración del intervalo (Duration) y las variaciones de energía potencial (DeltaPE) y cinética (DeltaKE):
Aero-Loss + Rolling-Loss = suma(Eta * Power * Duration) + DeltaPE + DeltaKE
utilizando la aproximación estándar que considera únicos y constantes el área de resistencia aerodinámica (CdA) y el coeficiente global de resistencia a la rodadura (Crr):
Aero-Loss = suma(0.5 * Rho * HeadWind^2 * Distance * CdA)
Rolling-Loss = suma(Mass * g * Distance * Crr)
donde Mass es la masa total del ciclista y su bicicleta, g la aceleración de la gravedad y Distance=v*dt, con v=velocidad y dt=duración del intervalo.
suma(*) es la acumulación sobre todos los intervalos de grabación correspondientes al segmento bajo consideración (una aproximación de primer orden a la integral).
La variación de energía potencial y cinética se puede calcular en función de la altimetría inicial y final (initalAlt y finalAlt) y la velocidad inicial y final (initialVel y finalVel):
DeltaPE = M * g * (initialAlt - finalAlt)
DeltaKE = 0.5 * M * (initalVel^2 - finalVel^2)
De manera que si tenemos N segmentos, tenemos N ecuaciones de la forma:
X1 * CdA + X2 * Crr = Egain
donde
X1 = suma(0.5 * Rho * HeadWind^2 * v*dt)
X2 = suma(Mass * g * v*dt)
Egain = suma(Eta * Power * Duration) + M * g * (initialAlt - finalAlt) + 0.5 * M * (initalVel^2 - finalVel^2)
los parámetros desconocidos son CdA y Crr, de manera que con dos segmentos podríamos tener una única solución pero, en general, es conveniente tener varios segmentos independientes y buscar la solución que mejor aproxime a todos ellos (mejor en este caso es en el sentido de minimizar el error medio cuadrático).
En forma matricial, utilizando una notación tipo Matlab con X = [X1 X2], tenemos:
X * [ CdA ; Crr ] = Egain
pre-multiplicando por la traspuesta de X (X'):
X' * X [ CdA ; Crr ] = X' * Egain
si llamamos A = X' * X y B = X' * Egain:
A * [ CdA ; Crr ] = B
llegamos a un sistema de 2 ecuaciones con dos incógnitas que se puede resolver para obtener una estimación de CdA y Crr.
El código C++ que implementa este mecanismo está incluido en este commit del código fuente de Golden Cheetah V3.
 La versión 3 de Golden Cheetah presenta una interfaz de usuario mejorada y varias funciones nuevas, entre ellas la posibilidad de realizar una estimación automática del área de resistencia aerodinámica (CdA) y el coeficiente de resistencia a la rodadura (Crr) utilizando datos de pruebas de campo. La metodología propuesta por el Dr. Robert Chung e incluída en el módulo Aerolab de Golden Cheetah por Andy Froncioni, está aumentada en la versión 3 con un mecanismo de estimación de parámetros de mi autoría que se describe a continuación.
La versión 3 de Golden Cheetah presenta una interfaz de usuario mejorada y varias funciones nuevas, entre ellas la posibilidad de realizar una estimación automática del área de resistencia aerodinámica (CdA) y el coeficiente de resistencia a la rodadura (Crr) utilizando datos de pruebas de campo. La metodología propuesta por el Dr. Robert Chung e incluída en el módulo Aerolab de Golden Cheetah por Andy Froncioni, está aumentada en la versión 3 con un mecanismo de estimación de parámetros de mi autoría que se describe a continuación.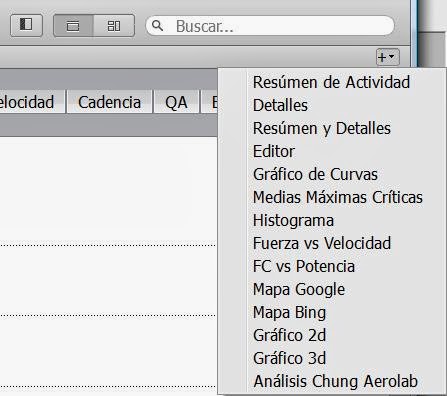











14 comentarios