 En esta primer parte analizamos los fundamentos en que se apoya la utilización de pruebas de campo para determinar el área de resistencia aerodinámica del ciclista y su bicicleta mediante pruebas de campo utilizando un medidor de potencia y un método analítico, publicado en la literatura científica, cuyos resultados han sido validados contra los resultados obtenidos en el tunel de viento, se incluye la referencia a las instrucciones detallas para realizar las pruebas y una planilla Excel para calcular los resultados.
En esta primer parte analizamos los fundamentos en que se apoya la utilización de pruebas de campo para determinar el área de resistencia aerodinámica del ciclista y su bicicleta mediante pruebas de campo utilizando un medidor de potencia y un método analítico, publicado en la literatura científica, cuyos resultados han sido validados contra los resultados obtenidos en el tunel de viento, se incluye la referencia a las instrucciones detallas para realizar las pruebas y una planilla Excel para calcular los resultados.
En la segunda parte presentamos un método gráfico cuya utilización es más sencilla y se adapta a una variedad mayor de lugares de prueba.
Modelo de la potencia en el ciclismo
La técnica que vamos a comentar se origina en un modelo de energético del ciclismo en el que se detalla en que se utiliza la potencia generada por el ciclista y que ya hemos comentado, incluyendo las contribuciones relativas de cada uno de los términos, en una nota anterior (ver punto 3.1 en Potencia y Aerodinámica en el Ciclismo). El modelo completo se presenta en forma detallada en la imagen inicial de esta nota tal como fue planteado en la publicación de Martin y otros que figura al final como ref. 1, el tamaño está elegido intencionalmente para tratar de no asustar a los lectores poco afectos a las ecuaciones, los interesados lo pueden ampliar para verlo completo.
En ese trabajo el grupo de investigadores evaluó el Área de Resistencia Aerodinámica (CdA o Área Frontal Efectiva) de 6 ciclistas en túnel de viento y luego realizó pruebas de campo en una calle lateral de un aeropuerto cuya pendiente era conocida y en la que midieron la velocidad y dirección del viento realizando múltiples pasadas en un tramo recto de 472m midiendo velocidad y potencia con un SRM.
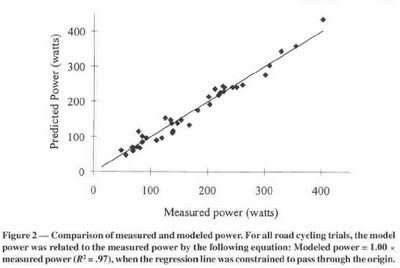
El siguiente gráfico muestra que la potencia calculada de acuerdo al modelo en función de dichos datos y la potencia medida por el SRM tienen un margen de error relativamente pequeño, del orden del error de medición del instrumento, lo que sirvió para confirmar la validez del modelo y la forma de obtención de los parámetros (Ref. 1):
Modelo simplificado de dos parámetros
En un trabajo de 2006 (ver ref. 2) Martin y sus colaboradores realizaron una modificación al modelo para reducir la cantidad de parámetros consolidando en un coeficiente de resistencia global la resistencia al rodamiento de los neumáticos y de los rodamientos e integrando al Área de Resistencia Aerodinámica (CdA) la contribución de los rayos de las ruedas en rotación que previamente habían considerado de manera separada:


Obtención de los parámetros por Análisis de Regresión
La escasa cantidad de datos para cada ciclista (6) dificulta obtener valores estables para el coeficiente de resistencia a la rodadura, para resolver este problema realizaron un análisis en dos pasos.
En el primer paso utilizaron obtuvieron los valores de ambos coeficientes para cada uno de los ciclistas, considerando que con las mismas ruedas y superficie, la resistencia a la rodadura (que ahora incluye la pequeña contribución de los rodamientos) debería ser la misma, obtuvieron un valor promedio que en el segundo paso de regresión utilizaron para determinar el CdA de cada ciclista:
El CdA obtenido por este método no es estadísticamente diferente al determinado en el túnel de viento, los valores individuales para cada ciclista se muestran a continuación (ref.2):

Precisión del método
En una publicación en su blog el Dr. Andrew Coggan (A challenge to cycling aerodynamicists) reporta la detección de diferencias de 0,0015m^2 mediante pruebas de campo sin viento utilizando análisis de regresión, suficiente como para detectar la diferencia debida al cambio de tamaño de la esfera entre las dos configuraciones de la siguiente foto:

Aplicación Práctica
La aplicación práctica de este método requiere contar con un medidor de potencia confiable (SRM, PowerTap, Quark) correctamente calibrado y una recta de al menos 400m sin obstáculos llana (o de pendiente conocida) idealmente en un día sin viento o con el menor viento posible (medir la velocidad del viento en la dirección de la prueba ayuda pero sin viento es lo ideal).
Es necesario obtener el peso total del ciclista con su bicicleta en las condiciones de la prueba.
Además es necesario conocer la temperatura, humedad relativa y presión atmosférica para calcular la densidad del aire, sino se cuenta con el instrumental adecuado se pueden consultar estos datos de la estación meteorológica más cercana.
La prueba consiste en recorrer la recta 6 veces, cada una a una velocidad diferente lo más constante posible, comenzando desde una velocidad muy baja y terminando a la velocidad más alta que se pueda mantener en forma segura en el área de prueba.
Los datos de cada prueba se obtienen del medidor de potencia tomando un parcial (lap) en cada pasada y son la velocidad inicial, promedio y final, duración y potencia promedio de cada pasada.
La descripción detallada del procedimiento de prueba se encuentra en Aerodynamic Drag Area of Cyclists Determined with Field-Based Measures y los datos se ingresan en la planilla CdA_calculator, que incluye una hoja para el cálculo de la densidad del aire, en la que es necesario ingresar un valor estimado para el coeficiente de resistencia basado en la superficie y los neumáticos utilizados, la planilla calcula el valor del CdA, el intervalo de confianza de ese parámetro y el grado de ajuste de los datos que debe ser superior a 0.98 para que el parámetro calculado sea útil:

El método comentado permite realizar determinaciones cuantitativas del comportamiento aerodinámico del ciclista y su bicicleta sin necesidad de recurrir al túnel de viento, algo que tiene un costo elevado y no es de fácil acceso en la mayoría de los países, la principal ventaja de estas pruebas es poder realizar comparaciones con otros atletas o con si mismo cuando se realizan cambios de posición y/o de equipamiento de manera de determinar si el cambio tuvo un efecto positivo, negativo o neutro y de que magnitud.
En ausencia de viento y con suficiente cuidado por los detalles se puede lograr una precisión comparable a la del túnel de viento.
Si bien el protocolo no es particularmente complicado es relativamente laborioso (tener en cuenta que hay que completarlo para cada configuración y/o posición que se quiere probar) y no permite determinar el coeficiente de resistencia a la rodadura sin aumentar en un buen número la cantidad de pasadas de prueba y modificar el método de cálculo.
Por último es un método analítico y, probablemente, muchos de los lectores no se sentirán especialmente cómodos con un procedimiento de este tipo de manera que en la segunda parte de esta nota analizamos una alternativa que es más flexible en cuanto a la elección del lugar de pruebas y es más sencillo/intuitivo por tratarse de un método gráfico.
Referencias
1.- Martin JC, Milliken DL, Cobb JE, McFadden KL and Coggan AR. Validation of a mathematical model for road cycling power. J. Appl. Biomech. 14:276–291, 1998.
2.- Martin JC, Gardner AS, Barras M, Martin DT. Modeling sprint cycling using field derived
parameters and forward integration. Medicine and Science in Sports and Exercise 38, 592-597, 2006.











5 comentarios